
Physics 232B -- Quantum Field Theory II
Spring 2022

shortcut to Homework Assignments
shortcut to References and Reading Recommendations
shortcut to List of Reading Assignments

 Basic Info Basic Info
Lectures:
Time: Tue and Thu, 9:40-11:00am.
Place: Lectures were delivered remotely live via Zoom from January 18; however, since February 1 we are back in person :) in 402 Physics South.
Discussion sessions:
Thursdays, 3:40-4:30pm, 402 Physics South.
Lecturer: Petr Hořava (email: horava@berkeley.edu)
Office: 401 Physics South.
Office hours: Effective from March 1, 2022, I have moved my office hours to Tuesdays 2:00-3:00pm. (On those rare weeks when I cannot make it in this time slot, we will use the alternate day/time of Thursday, 2-3pm.)
GSI: No.

 Syllabus Syllabus
In this advanced course, we will develop a more systematic understanding of Quantum Field Theory, building on the basics that you have learned in Physics 232A (or equivalent), as taught for example in Fall 2021 by Yasunori or in Fall 2020 by me. The subject of Quantum Field Theory is vast, with applications in virtually all areas of physics (and beyond) -- wherever many-body systems with fluctuations are involved. Ideas, methods and techniqes of QFT are now the prevalent language of theoretical physics, no longer confined only to high-energy particle physics: QFT is the go-to language and tool in particle phenomenology, condensed matter physics, equilibrium and non-equilibrium statistical mechanics, mesoscopic and AMO physics, quantum gravity, string theory and cosmology, with ramifications in mathematics and other fields. My aim is to stress this interdisciplinary nature of this fundamental theoretical "calculus of QFT" across subfields.
The focus will again be two-fold: To continue developing a strong technical understanding and mastery of the theoretical techniques involved, while simultaneously getting the "big picture" of understanding the role of QFT in describing the behavior of many-body systems and cooperative phenomena. The "big picture" that I will focus on will stress two main concepts in QFT:
(1) Renormalization (especially as covered by the concept of the renormalization group),
and
(2) Symmetries (both global and gauge symmetries).
Much of modern QFT deals with the mutual interplay of these two concepts, and we will illustrate this by focusing on several specific themes more deeply.
Here are the five major themes, with some more details on the specific topics that we will discuss:
1. Systematics of renormalization and the renormalization group. Renormalized perturbation theory. Evaluating loops and counterterms. Renormalization group, Callan-Symanzik equation. Relation of QFT to critical phenomena. QFT at finite temperature. Nonperturbative propagators, spectral representation. Path integral versus canonical Hamiltonian methods. Unitarity, Cutkosky rules, relation to Schwinger-Keldysh nonequilibrium formalism.
2. Symmetries in QFT. Global symmetries, gauge symmetries, and their interplay with renormalization. The main focus will be on non-Abelian Yang-Mills gauge theories, and their quantization. Faddeev-Popov ghosts, BRST quantization (including a brief look at the anti-bracket and the BRST-BV approach). Asymptotic freedom. Spontaneous symmetry breaking, Higgs mechanism. Renormalization of Yang-Mills. Quantum anomalies.
3. Nonperturbative techniques. Focus on importance of topological invariants. Examples: Solitons, instantons, large-N expansion. Nonperturbative dualities between QFTs. Stable Fermi surfaces in Fermi-like liquids. Basics of topological insulators and edge states in condensed matter.
4. Holographic dualities, intro to AdS/CFT correspondence. While AdS/CFT and holography originated from string theory, we can now teach its basics without requiring any string-theory pre-requisites. Elements of gauge-gravity duality, holographic renormalization, condensed-matter aspects of AdS/CFT correspondence, connection to Quantum Information Theory etc.
5. Effective field theories (EFTs). More on the Wilsonian approach to EFT and renormalization group. Quantum gravity and cosmological inflation as examples of EFT. Technical Naturalness and hierarchy puzzles in Nature (examples: Higgs mass hierarchy problem, cosmological constant problem, eta problem of cosmological inflation, resistivity in hgh-temperature superconductors).
Overall, I expect that the exact focus of the various parts of this course will be determined interactively, based on my polls of the research interests of the students who will register. Based on the level of interest, additional topics can be added (or subtracted) from this list, depending on the feedback that I will get from the course participants.

 Required and Recommended Textbooks Required and Recommended Textbooks
There are two required textbooks:
M.E. Peskin and D.V. Schroeder, An Introduction to Quantum Field Theory (Perseus, 1995),
and
A. Zee, Quantum Field Theory in a Nutshell, 2nd Edition (Princeton U. Press, 2010).
I shall refer to them as [PS] and [Zee] from now on.
In addition, there are many possible recommended texts, of which I will now mention only three. First,
S. Weinberg, The Quantum Theory of Fields, Volumes 1 and 2 (Cambridge U. Press),
is a brilliant resource, focused on the fundamental principles and properties of relativistic QFT as developed primarily in particle physics. This semester, it will be Volume 2 that will be most relevant to us.
M.D. Schwartz, Quantum Field Theory and the Standard Model (Cambridge U.P., 2014).
This book can be viewed as an updated version of [PS], with many new modern aspects of QFT and particle theory covered in extra detail (including for example Effective QFT).
F. Gelis, Quantum Field Theory: From Basics to Modern Topics (Cambridge, 2019).
This book is great at stressing the interplay between equilibrium and non-equilibrium QFT, Schwinger-Keldysh formalism and its uses, and the connections between similar QFT concepts in condensed matter, particle physics, etc.

 Prerequisites Prerequisites
Physics 232A: Quantum Field Theory I (or equivalent). In particular, Yasunori's 232A from Fall 2021 is the precise level of the required pre-requisite this semester.
And, I should say, no prior knowledge of string theory required (even for the part of the course where we will discuss AdS/CFT correspondence)! On the other hand, some rudimentary knowledge of classical general relativity will at times be useful.

 Discussion Sessions, Homeworks, Reading Assignments Discussion Sessions, Homeworks, Reading Assignments
The structure of the Discussion Sessions will be very similar to my 232A: QFT II that I taught in Spring 2021: First we will have a few weekly Homework Assignments, which will be due in one week, and whose solutions will be discussed in our Discussion Sessions. After that, starting after Spring Break, we will switch to Discussion-Session presentations of Reading Assignments by the enrolled students. The list of Reading Assignments has been posted here. For making your selection, please follow the instructions provided on that webpage.
IMPORTANT: In order to give everyone enough time to review the offered papers peacefully before having to make your choices, I impose a moratorium on the sign-up process, until Wednesday, March 9, Noon PST. Please do not send me your request emails before that time, all emails that will arrive before the deadline of March 9 Noon will be ignored.
No paper will be assigned to more than one student. The final grade will be a combination of the performance on homeworks, participation in class, and the presentation of the Reading Assignment in the Discussion.

 References and Recommended Reading References and Recommended Reading
Here I will post, on a weekly basis, the references to the appropriate parts of our main textbooks or other leading materials (from arXiv etc), which are most relevant to the material covered in lectures. Plus, I may occasionally post additional interesting references for further optional reading.
Week 1: We introduced the method of path integrals. The corresponding parts of the textbooks are: Ch. 9 of [PS], Ch. I.2 and following sections in [Zee]. Some of my additional material (such as the fractal dimension of the typical configuration in the path integral) is well presented in the beautiful, comprehensive (but expensive) book by
J. Zinn-Justin, Quantum Field Theory and Critical Phenomena (Oxford U. Press, 2002).
Week 2: We continued developing the path integral methods. The main reference continues to be Ch. 9 of [PS] (and various sections of Ch. I of [Zee]). The example of a particle on a circle, which illustrates the importance of summing over nontrivial topological sectors in the path integral, can be found in Zinn-Justin's book cited above.
Week 3: We finished developing the basic path integral methods, and applied them to field theories. We defined the (Berezin) integral over classical anticommuting (=Grassmannian) variables, and studied the Gaussian integrals for them, so that we could re-derive Feynman rules for fermions using the path integral language. We illustrated the notion of the renormalization group flow, renormalization-group fixed points, and even crossover phenomena, using some simple free field theory examples.
Week 4: We have now begun the "Systematics-of-Renormalization" theme. The main references are Ch. 10 of [PS], but also bits and pieces from the earlier chapters: For example, the exact propagator is discussed in Ch. 7.1, and the basic rules for evaluating loop diagrams are summarized in Ch. 6.3 of [PS].
We studied the expected nonperturbative analytic structure of the exact propagator, and checked it for the Dirac propagator in QED at one loop. We discussed the 1-particle irreducible (1PI) diagrams, and their resummation into the all-orders exact propagator.
Week 5: We defined the superficial degree of divergence for any diagram, and studied its behavior for renormalizable vs nonrenormalizable theories. For renormalizable ones, a finite number of normalization conditions for the renormalized amplitudes is required in order to render the theory finite to any order, at least in principle. These normalization conditions require the choice of a "subtraction point," a scale related to the RG scale. We presented the systematics of renormalized perturbation theory, introduced the notion of "counterterms", and formulated Feynman rules for them. We also discussed 't Hooft's notion of "Technical Naturalness," and illustrated it by looking at masses of scalars vs spinors. The original reference to Technical Naturalness is:
G. 't Hooft, Naturalness, Chiral Symmetry, and Spontaneous Chiral Symmetry Breaking, NATO Sci. Ser. B 59 (1980) 135,
which has been reprinted in the collection
G. 't Hooft, Under the Spell of the Gauge Principle (World Scientific, 1994).
Here is the correlation of the topics discussed in our Thursday lecture with the chapters in [PS] (and [Zee]). Renormalized perturbation theory for the scalar field: Ch. 10.2; for QED: Ch. 10.3. The generating functional of (all and connected) Green's functions: Ch. 9.2; the effective action and effective potential (in the sense of high-energy theory): Ch. 11.3; its one-loop computation: Ch. 11.4. The effective potential for the Coleman-Weinberg example is nicely discussed also in [Zee], Ch. IV.3.
Week 6: The example of the O(N) invariant nonlinear sigma model that we presented in class on Tuesday is discussed in [PS], Ch. 13.3. In particular, the exact large-N solution of this model (also discussed in class) is discussed in [PS] on pp. 463-6. See also the introductory sections (in particular Section 2.1) of
J.M. Maldacena, TASI 2003 Lectures on AdS/CFT, arXiv:hep-th/0309246,
a great resource which will (later on) be our primary reference for the introduction to holography and AdS/CFT correspondence.
The large-N expansion for theories with matrix-valued fields is presented in Maldacena's TASI lectures cited above, and also in Ch. VII.4 of [Zee].
Week 7: The phenomenological approach to holography and the rudimentary features of the AdS/CFT correspondence, which we discussed in class on Tuesday, follow largely Maldacena TASI lectures. The Wilsonian approach to renormalization is discussed in Ch. 12.1 of [PS], Ch. VI.8 of [Zee], and beautifully in the following pedagogical review paper,
R. Shankar, Renormalization Group Approach to Interacting Fermions,
a paper which also contains a detailed discussion of the Wilsonian renormalization group approach to nonrelativistic Fermi liquids (which will be discussed in class on Thursday this week).
Week 8: We wrapped up our discussion of Wilsonian renormalization in the Fermi liquid: The usual Step 1 and Step 2 of the Wilsonian procedure (first, integrate out a shell of DoF, then rescale and compare) need to be preceeded by Step 0 (which is usually absent in the relativistic theories): Identify the correct ground state, to determine what you will scale towards in the RG steps. Here, the scaling is towards the Fermi surface, and therefore has a nice description in momentum space, but not so nice in coordinate space: No simple rescaling of space and time! Again, the main reference is Shankar's review, cited above.
To prepare for the quantization of Yang-Mills, we discussed the important question of symmetries of the effective action: If the action and the path-integral measure are invariant under a symmetry, is the effective action invariant under the same symmetry? Usually, you hear that the answer is "yes", but as shown in Ch. 16.4 of [Weinberg, Vol. 2] (which we followed in class), the answer is more interesting, for symmetries that act more than linearly on fields.
With this preparation, we then started our systematic quantization of non-Abelian Yang-Mills theories and, more generally, any gauge theories with a simple closed symmetry algebra. The main reading references for Yang-Mills and related things are: Ch.15 and 16 of [PS], Ch. 25 and 26 of [Schwartz], and Ch. 15 (and for the more advanced things also 16 and 17) of [Weinberg, Vol. 2].
Week 9: More quantization of Yang-Mills. The reference we used for the general presentation of the BRST quantization of any gauge theory with a closed Lie algebra of gauge symmetries was Joe Polchinski's String Theory book, Volume 1, Ch. 4.2. For the specific applications to Yang-Mills, see again the chapters of [PS], [Schwartz] and [Weinberg] mentioned above in bold-face. The correct Hamiltonian starting point for the Yang-Mills quantization (as originally taken by Faddeev and Popov) is properly explained in
L.D. Faddeev and A.A. Slavnov, Gauge Fields. An Introduction to Quantum Theory (Routledge, 1991).,
and also in [Weinberg, Vol. 2, Ch. 15].
For those who wish to learn a lot more about the quantization of more general classes of gauge theories, the tour-de-force exposition of the subject is the legendary book
M. Henneaux and C. Teitelboim, Quantization of Gauge Systems (Princeton U. Press, 1994).
For the Cartan classification of Lie algebras in the A,B,...,G series, see for example:
A. Zee, Group Theory in a Nutshell for Physicists (Princeton U. Press, 2016).
For a review of the fascinating omnipresence of the ADE classification across various fields of mathematics (and elsewhere), see
M. Hazewinkel et al, The Ubiquity of Coxeter Dynkin Diagrams (An Introduction to the ADE Problem), or
K. Siegel, Ubiquity of ADE Classifications in Nature.
Week 10: Spring break. Enjoy!
Week 11: We continued the analysis of renormalization and RG at one loop in Yang-Mills, including the calculation of the beta function in QCD. The main reference was Chapter 26 of [Schwartz] (and the additional resources as mentioned above). The discussion of quantum anomalies, their Wess-Zumino self-consistency conditions, their BRST interpretation, and the Stora-Zumino descent equations followed [Weinberg, Vol.2], Chapter 22.6.
Week 12: Having studied Yang-Mills theories now in some detail, we have returned to holography and AdS/CFT correspondence. The main resource has been Maldacena's TASI lectures paper, as cited above.
In addition, I would like to recommend two well-written books on AdS/CFT and holography:
M. Ammon and J. Erdmenger, Gauge/Gravity Duality, Cambridge U.P., 2015
(This book is quite detailed in technical aspects of the story, and dilligently written. A good reference for more details on the basics of AdS/CFT and other gauge/gravity dualities.)
And the second one is:
J. Zaanen et al., Holographic Duality in Condensed Matter Physics, Cambridge U.P., 2015
(This one is very different in style: Very inspiring, full of big ideas, painted in much larger, not so technically detailed, brushstrokes.)
Week 13: We continued our analysis of AdS/CFT correspondence, holography, and holographic renormalization. The go-to reference are again Maldacena's TASI lectures cited above, plus for nonrelativistic holography, Lifshitz gravity and related phenomena, we used my 2016 Schladming lectures, specifically
lecture two. We also discussed how finite-temperature effects manifest themselves on both sides of the gauge/gravity duality, and how confinement on the gauge theory side corresponds to geometries "capping themselves off" in the bulk on the gravity side.
Since in the weakest form of the holographic duality, the gravity side is treated as a semiclassical effective field theory, we then started a systematic discussion of the general concepts of effective field theories, one of the most universal modern approaches to many-body systems.
I recommend two specific references for effective field theories:
J.F. Donoghue, The Effective Field Theory Treatment of Quantum Gravity, 2012 Petropolis lectures;
and the recently published textbook
C.P. Burgess, Introduction to Effective Field Theory: Thinking Effectively about Hierarchies of Scale, Cambridge U.P., 2020.
|
|

 Homework Assignments Homework Assignments
Homework assignments will be posted here on Tuesdays, around noon, and will be due in one week after posting, on Tuesday in class. Most homeworks will be assigned by referring to specific Problem numbers from either Zee's book [Zee] (important: we will use 2nd edition!), or Peskin-Schroeder [PS].
HW1 (posted Tue, Jan 25; due on Tue, Feb 1, in class): Problems I.2.1 and I.2.2 from [Zee] (on p. 16); Problems 9.2(a) and 9.2(b) from [PS] (on pp. 312-3).
HW2 (posted Tue, Feb 1; due on Tue, Feb 8, in class): Problem I.3.3 from [Zee] (on p. 24); Problems 9.2(c) and 9.2(d) and 9.1(a) from [PS] (on pp. 312-3).
HW3 (posted Tue, Feb 8; due on Tue, Feb 15, in class): First, as a reminder on how to evaluate simple loop diagrams, read Appendix 1 and 2 of Chapter III.1 of [Zee] (pp.167-8), and Appendix D of [Zee] (pp. 538-40). Then solve Problems III.1.2 and III.1.3 from [Zee] (p. 168), problem III.3.1 from [Zee] (p. 181); and Problems 11.3(a), 11.3(b) and 11.3(c) from [PS] (on p. 390).
HW4 (posted Tue, Feb 15; due on Tue, Feb 22, in class): Problems III.3.2, III.3.3 and III.3.4 from [Zee] (p. 181), and Problem 10.2(a) from [PS] (pp. 344-5).
(Of course, the "Weisskopf phenomenon" discussed in Problems III.3.3 and III.3.4 of [Zee] is just an example of Technical Naturalness in practice.)
HW5 (posted Tue, 2-22-22; due on Tue, March 1, in class): Problems 11.3(d), 11.3(e) and 11.3(f) from [PS] (p. 391).
HW6 (posted Tue, March 1; due on Tue, March 8, in class): Problem 13.3(a,b,c,d) from [PS] (p. 466-8). In addition, two problems related to ribbon diagrams and triangulations of surfaces:
(i) Using any triangulation of your choice, calculate the Euler number of the torus, and the Euler number of a closed oriented compact surface with two handles.
(ii) Determine the genus of the closed oriented compact surface which is associated with the following ribbon diagram in a theory of NxN matrices:
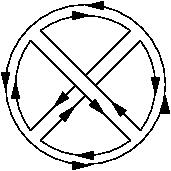 (This association we defined in class as the lowest-genus surface on which the ribbon diagram can be drawn, or, equivalently, as the order in the 1/N expansion at which the diagram contributes.)
(This association we defined in class as the lowest-genus surface on which the ribbon diagram can be drawn, or, equivalently, as the order in the 1/N expansion at which the diagram contributes.)
|
Tue, March 8: There will be no more weekly HW assignments. Instead, this week the task is for the students to browse the posted selection of Reading Assignments, and starting at Noon of Wed, March 9, request their choice by email to me, on a first-come, first-served basis.
|
|
 horava@berkeley.edu
horava@berkeley.edu
|

 horava@berkeley.edu
horava@berkeley.edu

 horava@berkeley.edu
horava@berkeley.edu