Physics 234A: String Theory I
Fall 2019
shortcut to Homework Assignments

 Basic Info Basic Info
Time and place for lectures: Mondays, 2:10pm - 3:30pm, 325 Le Conte,
and Fridays, 2:10pm - 3:30pm, 402 Le Conte.
Time and place for discussions: Starting the week of October 2, the discussions will be on Wednesdays, 2:00-3:00pm, in 200 Le Conte.
Instructor:
Petr Hořava
(email: horava@berkeley.edu)
Office: 401 Le Conte Hall.
Office hours: Tuesdays 1-2pm.
GSI: Chitraang Murdia (shared with Prof. Nomura's 232A course).

This course will give a thorough introduction to modern string theory.
In the past two decades or so, string theory has become the dominant
theoretical framework for addressing questions about the fundamental
structure of matter in our Universe. It has produced many new ideas and
insights in other fields of physics,
ranging from particle phenomenology to quantum gravity, cosmology, and
substantially even to condensed matter systems.
Some of this surprising power of string theory is logically explained by the
fact that string theory represents a natural extension or completion of the
language of quantum many-body systems and quantum field theory, which makes
it relevant in all those diverse areas where the methods of many-body physics
play an important role. Basics of string theory should now be in every
theorist's vocabulary, regardless of the specific field of physics.
Our main focus in the first semester will be on what I call the "alphabet" of string theory, and our goal will be two-fold: First, we will develop
some practical understanding of the basic elements and techniques of string
theory at the technical level. Simultaneously, we will also focus on understanding the "big
picture" -- how string theory produces new ideas and techniques relevant to
other areas of physics besides particle phenomenology and quantum gravity.
Throughout the semester, I will also point out some of the open questions
and puzzles of our field.
This semester will be quite fast-paced, and hopefully will prepare us for the second semester of string theory 234B in Spring 2020 (which will also be taught by me! :) In the second semester, we will explore string theory "beyond its basic alphabet": 234B will focus specifically on various advanced topics such as influential applications of string theory to condensed matter, cosmology and mathematics. We will study AdS/CFT correspondence and holography, topological strings and topological QFTs, effective field theory approach to inflation, the apparent challenges for string theory in quantum gravity context, and/or other topics whose precise selection will be determined interactively with the students who will register for that 234B course.
In this first semester, our 234A will specifically cover the following five areas:
I. Introduction: Why strings?
II. The bosonic string.
III. Superstrings, heterotic strings, supergravity.
IV. D-branes.
V. M-theory and nonperturbative string-string dualities.
The style will be somewhat similar to the style of my course taught in
Fall 2008,
Fall 2009,
Fall 2011, and
Fall 2015.
However, as the field is evolving, we will take a novel, fresh
look at some of the basic questions and applications of string theory in the
context relevant for current research.
The main textbook is going to be
K. Becker, M. Becker and J.H. Schwarz, String Theory and M-Theory. A Modern Introduction (Cambridge University Press, 2006).
We will occasionally use other resources, including the two volumes of Joe Polchinski's book, the classic two volumes of Green-Schwarz-Witten, or the newer book by Elias Kiritsis (String Theory in a Nutshell), whose second and improved edition has just been published. Sometimes we will use review papers from the arXiv, especially for the more advanced topics (and later on in 234B).
 Prerequisites Prerequisites
In order to make Physics 234A accessible to a wide audience of students from
varying areas of physics and cosmology, I will develop the material from first
principles, such that the course can be taken without any prior knowledge of
quantum field theory. Thus, this course could be taken concurrently with
232A. Some basic understanding of quantum mechanics and relativity is
however assumed.
 Grading Policy Grading Policy
The final grade will be based on three things: 1. homeworks, 2.
participation in discussions (during discussion sessions as well as lectures),
and 3. the possible final exam. As I have done with similar classes in previous years, I will apply the "two-out-of-three" rule for the final grade -- briefly, it means that for a good grade (say an A) it is sufficientto do really well on two out of 1., 2. and 3. listed above; for example,
if you do great on homeworks and you interact well in discussion sessions and
lectures, you will be exempt from the final exam. (Other permutations work
as well.)
 Homework Assignments Homework Assignments
Homework assignments will be posted on this website weekly (or sometimes biweekly), on Fridays, after class, usually before 5pm. The assignments will be due in one week's time, on Friday, in class. Solutions will be presented by the students themselves and discussed interactively in the Discussion Sessions (run by me), usually in the week following the due date.
Most homeworks will be assigned from the list of Homework problems in
Becker&Becker&Schwarz ([BBS]), unless stated explicitly otherwise.
Occasionally, the assignment will contain also solved Exercises from [BBS];
if so, the students are encouraged to solve the problem before they look at
the solution in [BBS].
HW1: Just a reading assignment, nothing to physically turn in. The early days of string theory are nicely described in:
J.H. Schwarz, The Early History of String Theory and Supersymmetry, arXiv:1201.0981.
For an elementary and fascinating analysis of the simplest Veneziano amplitude, see the brilliantly written
Chapter 1.1 of M.B. Green, J.H. Schwarz and E. Witten,
Superstring Theory , Vol. 1.
HW2 (posted Sept 13, due Friday Sept 20 in class):
Problems 3.1, 3.2 and 3.3 from [BBS] (they are on page 106).
HW3 (due Friday Sept 27 in class):
Problem (1): Using any triangulations of your choice, calculate the Euler number of the torus, the Euler number of the cylinder (of finite length), and the Euler number of a closed oriented surface with two handles.
Problem (2): Determine the genus of the closed oriented surface which is associated with the following ribbon Feynman diagram in a theory of NxN matrices:
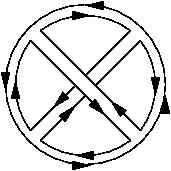
(Such an association is defined as we saw in class: The lowest-genus compact surface such that the diagram can be drawn on that surface; or equivalently the surface whose genus is equal to the order in the 1/N expansion at which that diagram contributes.)
Problem (3): Show that the so-called Nambu-Goto action of the bosonic string (given in Eqn. (2.11) on p. 24 of [BBS]) is invariant under worldsheet diffeomorphism transformations.
HW4 (due Friday Oct 4 in class): Problems 2.1(i), 2.3(i,ii), 2.5 and 2.6 from [BBS] (on pp. 53-6).
HW5 (because of the campus power outage, due Monday Oct 14 in class): Problems 2.4, 2.12, 2.13 and 2.15 from [BBS] (on pp. 55-7).
HW6 (due on Friday, Oct 25 in class): First, solve Exercises 3.1, 3.2, and 3.6 (on pp. 72-74 and 87 of [BBS]) before you look at the solutions provided in the book. Then solve Problems 3.4, 3.6, 3.7 and 3.10 (pp. 106-7 of [BBS]).
In Monday's lecture, I promised to post two very useful and time-tested review papers on the basic language and structure of CFT in two dimensions, here they are:
P. Ginsparg, Applied Conformal Field Theory, arXiv:hep-th/9108028,
and
P. Goddard and D. Olive, Kac-Moody and Virasoro Algebras in Relation to Quantum Physics, Int. J. Mod. Phys. A1 (1986) 303.
HW7 (due on Friday, Nov 1, in class): Exercise 3.5 (on pp. 80-81 of [BBS]), and Problems 3.11, 3.12 and 3.14 (on pp. 107-108 of [BBS]).
In addition, evaluate the BRST cohomology of the point-like particle with mass m discussed in class, and show that the cohomology contains two copies of the Hilbert space of this physical particle: One copy in the ghost sector with the arrow up, and one copy in the ghost sector with the arrow down.
HW8 (due on Friday, Nov 8, in class): First, Problems 3.13(i) and 3.13(ii) (p. 108).
Then, solve Exercises 3.8 and 3.9 (pp. 96-7 in [BBS]) without looking at the solutions.
Finally, derive the Virasoro-Shapiro amplitude for the scattering of N closed-string tachyons at tree level, as given in Eqn. (3.116) (and (3.117)) on p. 91-2 of [BBS]. [Hint: You have to keep track of the correct Jacobian from the gauge fixing of the residual finite-dimensional CKV symmetry group by choosing the fixed location of three out of the N vertex operators.]
HW9 (due on Friday, Nov 15, in class): Problem 6.5 (on p. 245 of [BBS] -- they talk about the bosonic "NS-NS" sector of superstring theory, but you should ignore this superstring context and solve this problem in the purely bosonic string, where the answer is identical, with their index "9" referring to our compactified 25-th spatial dimension of the bosonic string).
Exercise 7.3 (p. 280), Problem 7.9 (p. 293 of [BBS]).
HW10 (due on Friday, Nov 22, in class): Problems 4.1, 4.2, 4.3 and 4.4, from pages 144-5 of [BBS].
HW11 (due IN TWO WEEKS, on Friday, Dec 6, in class): Problems 4.7, 4.8, 4.11, and 4.13 from page 146 of [BBS]. (Problem 4.8 may look ad hoc, but it is a great elementary example of the so-called Firtz identities, which become much more involved in higher dimensions where you will really need them.)
Problems 5.3 and 5.8 from p. 185 of [BBS] (This last problem deals with the Green-Schwarz formulation of the superstring, which we will discuss in our lecture next week.)
|
Optional HW12 (no due date): This homework set is purely voluntary, and will not be collected by our GSI. Nevertheless, it gives a good practice for some of the concepts we have encountered in the heterotic string constructions: Exercise 7.10 (p. 289 of [BBS]), Problems 7.3, 7.4, 7.5 and 7.10(ii) (from pp. 292-4 of [BBS]). Enjoy!
|
|
 horava@berkeley.edu
horava@berkeley.edu
|